Difference between revisions of "Statistics: Comparing groups"
(Created page with "<big>'''Comparing groups: t-tests and ANOVAs'''</big> ==Overview== {| class="wikitable" |- | colspan="2" | '''''important terms:''''' |- | t-test | a simple test to compa...") |
m |
||
| (One intermediate revision by the same user not shown) | |||
| Line 92: | Line 92: | ||
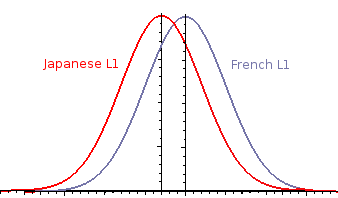
If there is no meaningful difference between the two groups, then they simply belong to the same sampling distribution--we have selected or sampled subjects from the same distribution of general L1 speakers. The two distributions are identical or almost identical--a clear overlap, where a clear-cut distinction between groups cannot be mathematically proven. | If there is no meaningful difference between the two groups, then they simply belong to the same sampling distribution--we have selected or sampled subjects from the same distribution of general L1 speakers. The two distributions are identical or almost identical--a clear overlap, where a clear-cut distinction between groups cannot be mathematically proven. | ||
| − | [[File: | + | [[File:Dist.comp.2.l1.png|350px]] |
With a statistical test, we would attempt to see if the data for French and Japanese L1 subjects constitute one or two distributions like these<ref name="ftn2">These statistical tests are based on the normal distribution, but the statistical calculations may use very slight modifications of the distribution. The t-test uses a form of the normal distribution tweaked for small samples, which is called the Student distribution. ANOVAs use the F-distribution for larger samples, named for R.A. Fisher, one of the founders of modern statistics. </ref>. In comparing groups and distributions, we do not just rely on comparing mean scores for groups, but a second important criterion: the variance for each group. If two groups are significantly different, the difference will manifest itself through different mean scores and/or difference amounts of variance (usually both). | With a statistical test, we would attempt to see if the data for French and Japanese L1 subjects constitute one or two distributions like these<ref name="ftn2">These statistical tests are based on the normal distribution, but the statistical calculations may use very slight modifications of the distribution. The t-test uses a form of the normal distribution tweaked for small samples, which is called the Student distribution. ANOVAs use the F-distribution for larger samples, named for R.A. Fisher, one of the founders of modern statistics. </ref>. In comparing groups and distributions, we do not just rely on comparing mean scores for groups, but a second important criterion: the variance for each group. If two groups are significantly different, the difference will manifest itself through different mean scores and/or difference amounts of variance (usually both). | ||
| Line 397: | Line 397: | ||
Scores or values on a variable can be expressed in terms of the standard deviation. And as a property of the normal distribution, 68% of the scores will fall within one SD below or above the mean, and 95% will fall within 2 SDs above or below the mean. This allows us to characterize scores in terms of the SD and the normal distribution. This also allows us to use SD values as cut-offs or as criteria for classifying scores or subjects into meaningful levels. We can convert these scores into numbers based on SD units, known as z-scores. | Scores or values on a variable can be expressed in terms of the standard deviation. And as a property of the normal distribution, 68% of the scores will fall within one SD below or above the mean, and 95% will fall within 2 SDs above or below the mean. This allows us to characterize scores in terms of the SD and the normal distribution. This also allows us to use SD values as cut-offs or as criteria for classifying scores or subjects into meaningful levels. We can convert these scores into numbers based on SD units, known as z-scores. | ||
| − | [[File: | + | {| |
| − | + | |- | |
| − | + | | [[File:Normal.dist.sd.percent.png|350px]] | |
| − | |||
| ± 1 SD = 68.27% of the set <br> | | ± 1 SD = 68.27% of the set <br> | ||
± 2 SD = 95.45%<br> | ± 2 SD = 95.45%<br> | ||
| Line 410: | Line 409: | ||
Once the mean and SD are known for a set of data, the scores (such as subjects' test scores or responses) can be standardized by expressing the score in terms of SD units. This is known as a z-score. The z-score is computed as follows, for a score ''x'' and a mean ''x̄:'' | Once the mean and SD are known for a set of data, the scores (such as subjects' test scores or responses) can be standardized by expressing the score in terms of SD units. This is known as a z-score. The z-score is computed as follows, for a score ''x'' and a mean ''x̄:'' | ||
| + | :[[File:Z.equals.xbar.sd.png]] | ||
| Line 512: | Line 512: | ||
Somewhat like an ANOVA or regression model, for measuring events at different times and correlations between times and events (e.g., measuring performance on a particular language skill over time, and including the times as a factor in the equation). More complex analyses would use whats known as a generalized liner model (GLM) instead of a standard ANOVA. GLM is a more sophisticated statistical test that would be preferred, since this handles time variables differently than other variables. | Somewhat like an ANOVA or regression model, for measuring events at different times and correlations between times and events (e.g., measuring performance on a particular language skill over time, and including the times as a factor in the equation). More complex analyses would use whats known as a generalized liner model (GLM) instead of a standard ANOVA. GLM is a more sophisticated statistical test that would be preferred, since this handles time variables differently than other variables. | ||
| − | : y = t<sub>1</sub>(b<sub>1x1</sub> ...) + t<sub>2</sub> (b<sub>1</sub>x<sub>1</sub> ...)... where t = measurement times | + | : y = t<sub>1</sub>(b<sub>1x1</sub> ...) + t<sub>2</sub> (b<sub>1</sub>x<sub>1</sub> ...)... ''where'' t = measurement times |
| Line 533: | Line 533: | ||
1. In a medical experiment, the outcome measured is whether the patient responds to a new drug or treatment. | 1. In a medical experiment, the outcome measured is whether the patient responds to a new drug or treatment. | ||
| − | :y = x | + | : y = x |
| − | :where x = drug dosage (0mg, 100mg, 500mg), and | + | : ''where'' x = drug dosage (0mg, 100mg, 500mg), and |
| − | :y = outcome: no improvement, slight improvement, moderate improvement, great improvement | + | : y = outcome: no improvement, slight improvement, moderate improvement, great improvement |
2. In a survey of how subjects feel about their level of L2 attainment, where numbers on a Likert scale survey represent these categories. | 2. In a survey of how subjects feel about their level of L2 attainment, where numbers on a Likert scale survey represent these categories. | ||
| − | :y = x | + | : y = x |
| − | :where x = motivation type: pragmatic, general intrinsic, or integrative (social), and | + | : ''where'' x = motivation type: pragmatic, general intrinsic, or integrative (social), and |
| − | :y = self-perception of L2 attainment: poor, so-so, good, high | + | : y = self-perception of L2 attainment: poor, so-so, good, high |
| Line 614: | Line 614: | ||
For a simple comparison of two groups, the t-test compares different scores between groups [x<sub>1</sub>, x<sub>2</sub>...], the standard deviation [s], and the n-size (number of subjects). | For a simple comparison of two groups, the t-test compares different scores between groups [x<sub>1</sub>, x<sub>2</sub>...], the standard deviation [s], and the n-size (number of subjects). | ||
| − | + | : [[File:T.eq.x1.x2.over.s.sqrt.n.png]] | |
An ANOVA works similarly, comparing the sum of squares (variance) overall with those of the different groups, e.g., treatment and control groups (plus error, or variance that can't be explained by the treatment effect). | An ANOVA works similarly, comparing the sum of squares (variance) overall with those of the different groups, e.g., treatment and control groups (plus error, or variance that can't be explained by the treatment effect). | ||
| Line 622: | Line 622: | ||
This is computed by comparing the overall variance, and the group means and variances. | This is computed by comparing the overall variance, and the group means and variances. | ||
| − | + | : [[File:F.eq.grp.mean.with.grp.var.png]] | |
| + | |||
| + | ''or'' | ||
| + | |||
| + | : [[File:F.eq.ms.between.ms.within.gif]] | ||
Latest revision as of 08:39, 19 October 2018
Comparing groups: t-tests and ANOVAs
Contents
1 Overview
| important terms: | |
| t-test | a simple test to compare two groups |
| ANOVA | analysis of variance; similar to the t-test, used for more complicated designs |
| mean | arithmetic average |
| variance | how individual scores or numbers (for a variable, especially for a dependent variable) differ from the mean value |
| standard deviation | the average amount of variance for a group (how much they differ from the mean, on average) |
| significant difference | a difference between two groups that is mathematically real, meaningful, or valid--meaning then that the independent variable has a real effect on or relationship with the dependent variable |
| probability | the likelihood that the mathematical difference between two groups is significant; the likelihood that the results are good, and not due to chance (reliable, not a fluke) |
| distribution | the mathematical pattern into which data points fall; usually they conform to known mathematical patterns known as distributions; different statistical tests are based on different distributions |
2 Comparing groups
When we formulate a research hypothesis, we are in essence comparing two groups. For example, let's take a hypothesis like this:
Hypothesis: French learners of English will outperform Japanese learners of English in reading syntactically complex sentences (assuming the same advanced proficiency level), in terms of sentence-final wrap-up times.
We are comparing French and Japanese learners of English, like so:
- y = x where y = reading times, and x = L1 group
We are also in effect comparing the above research hypothesis with a null hypothesis (that there is no difference between the two groups), which we are trying to disprove (as discussed in the hypothesis handout). When we compare groups, we want to see if one group is meaningfully different than the other, as shown by a statistical analysis. To prove this statistically, we look to see if the two groups are different in terms of their means (averages) and standard deviations (which will be explained below).
T-tests and ANOVAs are basically similar. A t-test is the simplest kind of test, which can be used for one independent variable with two groups; or if there is one independent variable that is a numerical (continuous) variable. For more complex designs, an ANOVA must be used--if there are three or more group levels in a variable, or if there are two or more independent variables.
| t-test | 1) one continuous variable
|
2) two groups (one categorical variable with two levels)
| |
| ANOVA | 1) comparing three or more groups
|
2) two or more independent variables
|
To understand how these tests work, we have to understand the following terms: distribution, variance, standard deviation, and probability. First, a t-value (for a t-test) or F-value (for an ANOVA) is calculated from the group means and variances; then from the t-value or F-value and the degrees of freedom (see below), the p-value is calculated.
3 Distributions
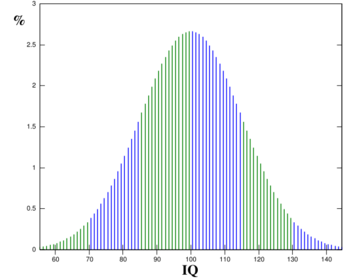
The likely distribution of values for the variables. For example, look at the distribution of IQ scores, which follow the standard bell curve shape. If you randomly select people and find their IQs, they will most likely fall near the middle--much more around the middle hump.
Many things measured in the natural world or in social sciences follow this distribution, known in common parlance as the bell curve, or in math and statistics, as the normal, standard normal (or Gaussian distribution, to be even more technical). People's scores will most often fall into the 85-115 range, followed by the 70-85 and 115-130 ranges, and very few fall into the extreme ends, above 130 or below 70. These ranges represent certain distances from the mean[1] (x̄ = 100) that are defined by standard deviations (see below).
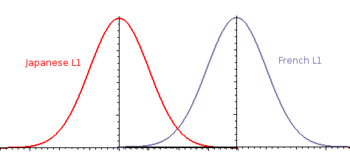
Many statistical tests assume the data fit a standard distribution. In experiments, we essentially compare two different groups in order to provide evidence for a hypothesis. If we have a hypothesis that French speakers will outperform Japanese speakers in a reading test of English as an L2, then we are comparing the distributions for the French and Japanese groups. If the hypothesis is true, then the French and Japanese actually constitute two different groups, statistically. Thus, each should belong to a separate, distinct distribution (one for French speakers, one for Japanese speakers). Statistical tests like t-tests or ANOVAs would test this and provide conclusive mathematical evidence for or against this hypothesis. If they are different groups, meaning that L1 has a significant effect, these groups would constitute separate, distinct distributions, like so.
The tails will likely overlap, but those are outliers or less common cases; as a whole, the two groups are distinct. Whenever we look to see if an independent variable has a real effect on an outcome (dependent variable), we often do so by comparing different groups (levels, categories) within the IV. If different groups within the IV have different effects on the DV, and these effects are large enough that they constitute different groups.
If there is no meaningful difference between the two groups, then they simply belong to the same sampling distribution--we have selected or sampled subjects from the same distribution of general L1 speakers. The two distributions are identical or almost identical--a clear overlap, where a clear-cut distinction between groups cannot be mathematically proven.
With a statistical test, we would attempt to see if the data for French and Japanese L1 subjects constitute one or two distributions like these[2]. In comparing groups and distributions, we do not just rely on comparing mean scores for groups, but a second important criterion: the variance for each group. If two groups are significantly different, the difference will manifest itself through different mean scores and/or difference amounts of variance (usually both).
4 Variance
An important part of the calculations in statistics tests involves variance. Let's look at the IQ test. Variance is the amount of variation between individual scores for a variable and the mean. For example, let's take IQ scores, where the mean = 100 points, but most individuals have scores above or below 100. There is a difference, or variation, or variance, between people's scores and the overall group mean of 100. Each individual's score varies from the overall group mean of 100. We subtract the individual score from the group mean (|100-x|) for the individual variance. Then we average all the individual variances for the average amount of deviation from the mean--the standard deviation. We can describe these differences in terms of deviations. Variance is actually the square of the deviation value, or the deviation is the square root of the variance[3].
| x= IQ score | deviation = (x̄-x) = (100-x) |
variance = (x̄-x)2 = (100-x)2 |
|---|---|---|
| 109 | 9 | 81 |
| 119 | 19 | 361 |
| 126 | 26 | 676 |
| 83 | 17 | 289 |
| 89 | 11 | 121 |
| 111 | 11 | 121 |
| 124 | 24 | 576 |
| 111 | 11 | 121 |
| 107 | 7 | 49 |
| 91 | 9 | 81 |
| 120 | 20 | 400 |
| 74 | 26 | 676 |
| 78 | 22 | 484 |
| 83 | 17 | 289 |
| 105 | 5 | 25 |
| 98 | 2 | 4 |
| 114 | 14 | 196 |
| 77 | 23 | 529 |
| 117 | 17 | 289 |
| 121 | 21 | 441 |
| 107 | 7 | 49 |
| 105 | 5 | 25 |
| 101 | 1 | 1 |
| 49 | 51 | 2601 |
| 73 | 27 | 729 |
| 85 | 15 | 225 |
| 99 | 1 | 1 |
| 84 | 16 | 256 |
| 101 | 1 | 1 |
| 110 | 10 | 100 |
| 112 | 12 | 144 |
| 116 | 16 | 256 |
| 102 | 2 | 4 |
| 85 | 15 | 225 |
| 90 | 10 | 100 |
| 87 | 13 | 169 |
| 131 | 31 | 961 |
| 88 | 12 | 144 |
| 140 | 40 | 1600 |
| 85 | 15 | 225 |
| sum (Σ) | 4007 | 611 | 13625 |
| mean (x̄) | x = 100.2 | s = 15.3 | s2 = 340.6 |
If we do this for a relatively large sample of the population--for a random sample of subjects--we can take the average of all the individual variances, and find that the sd=15 (for the Wechsler IQ test) or sd=16 (Stanford-Binet IQ test). This is true for all adults who have taken an IQ test. So they will all fall into the same distribution with the same standard deviation.
| politicians | grad students |
| 99 | 132 |
| 95 | 126 |
| 67 | 112 |
| 72 | 120 |
| 94 | 152 |
| 87 | 115 |
| 98 | 121 |
| 89 | 130 |
| 91 | 121 |
| 78 | 134 |
| 65 | 128 |
| 99 | 118 |
| 69 | 124 |
| 83 | 139 |
| 77 | 160 |
| 94 | 128 |
| 85 | 133 |
| 76 | 127 |
| 86 | 168 |
| 80 | 119 |
| politicians | grad students | |
| n | 20 | 20 |
| mean | 84.2 | 130.4 |
| standard deviation | 21 | 57.1 |
| median | 85.75 | 127.75 |
| sample variance | 609.2614 | 1588.651 |
The comparison in a t-test yields a t-value of t(1,38)=1.69, p<.0001. The important thing to look at is the p-value (these other numbers will be explained below). If the p-value is at or below 0.05 (p≤.05), then that is considered to be a significant difference. In social science and related fields, .05 is like the magic number for significance[4]. This means a significant, meaningful difference exists between both groups. This leads us to conclude definitively that grad students are significantly smarter than politicians.
4.1 Standard deviation units
Scores or values on a variable can be expressed in terms of the standard deviation. And as a property of the normal distribution, 68% of the scores will fall within one SD below or above the mean, and 95% will fall within 2 SDs above or below the mean. This allows us to characterize scores in terms of the SD and the normal distribution. This also allows us to use SD values as cut-offs or as criteria for classifying scores or subjects into meaningful levels. We can convert these scores into numbers based on SD units, known as z-scores.

|
± 1 SD = 68.27% of the set ± 2 SD = 95.45% |
Once the mean and SD are known for a set of data, the scores (such as subjects' test scores or responses) can be standardized by expressing the score in terms of SD units. This is known as a z-score. The z-score is computed as follows, for a score x and a mean x̄:
For example, an IQ of 120 is 1.3 SD units above the mean (20/15=1.33), 125 is 1.7 SD units (25/15=1.66) above the mean, and 130 is 2.0 SD units above.
5 Calculating the statistics
Stats tests essentially compare two or more groups to determine if they fall within the same distribution, and are thus the same thing, not different from each other--or fall into two separate normal distributions, and are thus separate entities. For example, in comparing two pedagogical techniques, we collect data such as student's scores on a post-test. If one is better than the other, they are different, and the students' scores are actually meaningfully different. Thus, scores from the two groups belong to two different normal distributions, and you can claim that the two are different, or that one is better. But if student scores are not meaningfully different, the scores follow the same distribution, and student performance is the same for both groups.
This meaningfulness in group difference is referred to as significant difference. Part of the stats results includes a p value, or probability value. This represents the probability that the two groups are the same (i.e., of the same distribution, not different distributions); or the probability that the different results between groups (e.g., different score results for the dependent variable) are due to random error rather than a real difference in groups. In the social sciences, we rely on a p=value of p<.05 as a standard cut-off for significance (p<.01 is a common criterion in medical research).
The results of a statistical test must be p<.05 to conclude that two or more groups are different, and that the independent variable has a real, meaningful, significant effect on the dependent variable. For example, a value of p=.04 translates to a mere 4% chance that the two groups are the same (thus, probably not the same), or a 4% chance that the results are due to pure chance rather than a real difference in groups--thus, a 96% likelihood that the groups are different, and thus, that the independent variable in question has a real effect, that is is a significant, meaningful factor.
5.1 Degrees of freedom
The p-value is computed from the t-value from a t-test or the F-value from an ANOVA; and from the degrees of freedom (see below). These look like so in the output--degrees of freedom (df) are usually reported in parentheses. There are two df numbers here. The first number in the parentheses is degrees of freedom for groups in the experiment, and the second one is for the number of subjects. Here is the example of the politicians versus grad students from above.
- t(1,38) = 1.69, p<.0001
- F(1,38) = 2.86, p<.0001
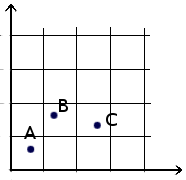
Degrees of freedom is a complex, theoretical, abstract complex; to simplify things, it has to do with the dimensionality of the variables--how many data points are available for mathematical comparison. In other words, it is a measure of the statistical power available to detect differences between groups. Imagine making a comparison between data points like these, which plot the relationship between x (the predictor variable) and y (the outcome variable). Here we have three points, and one point is used as a baseline for comparison. If A is used as a reference point for comparison, then with three points we can make two comparisons: B cf. A, and C cf. A. So the df is one less dimension than the number of items.
DF indicates how much statistical power we have. If we have more subjects, we have more data points for the variables, and more data points per group, and hence, more statistical power to detect potential differences between groups. So more df for subjects is preferred. However, more groups means less power--more groups would mean less power to detect differences, unless we then have more subjects. So fewer df for the number of groups is preferred. So in parentheses we have two df numbers:
- (df-groups, df-subjects)
We first have df for the number of groups in the experiment. This is the first number in the parentheses above. If L1 is a variable and we have three group (k=3, where k refers to the number of groups), so df for groups would be:
- df-groups): k-1 = 2-1 = 1
Then we have df for the number of subjects--this is the second number in parentheses. In a very simple design, it would be df = n-1 for each group. For the above example,
- df = N--k -1 (N = total #subjects, k = #groups)
- df = 40-2-1 = 38
This is equivalent to n-1 for each of the two groups ([20-1 = 19]x2 = 38). (For more complicated designs, calculating df gets more complicated.) And so for the above example, we saw the following:
- t(1,38) = 1.69, p<.0001
The statistical software calculates the t-value or F-value from the means and standard deviations / variances. The software then uses the t-value or F-value and the degrees of freedom to calculate the p-value. Again, the p-value must be at or below .05. This criterion number is referred to as alpha [α], and as mentioned, the alpha level or criterion is .05 in the social sciences (lower in other fields like medical research where significance is more critical due to life-and-death or health-related outcomes).
5.2 Post hoc tests
The results of the F-test are compared to the F-distribution values on a chart to determine significance (p). If an overall significant difference is found, then come follow-up or post hoc tests is performed along with the ANOVA. For example, in comparing three L1 groups (French, Chinese, Japanese), the basic ANOVA only tells us that L1 is a significant factor, that some kind of difference exists between groups. It does not tell us exactly where the difference(s) would be, if there are more than two groups. Thus, a post hoc (Latin: “after this,” i.e., after the fact) test is needed to look for specific contrasts among the different L1 groups. So we have the following post hoc contrasts to test for. # French Japanese
- French ≠ Chinese
- Chinese ≠ Japanese
There are different post hoc tests, which are basically similar (some may be better than others, but you can learn about these differences in a statistics course later). The most common post hoc tests are: Tukey's, Scheffe's, or Bonferroni's tests (also others, like Huyn-Feldt, Sidak's, Duncan's, LSD, Neuman-Keuls). This yields numerical output similar to t-test results, but again, the important thing to look for is the p-value for each contrast. For example, you might find a significant difference between French cf. Japanese, and French cf. Chinese, but not Chinese cf. Japanese, in the post hoc p-values.
5.3 Effect size
ANOVAs tell you if two or more groups are different. They do not tell you how different they are, or the strength of the relationship between x and y. To determine the degree of the relationship, a correlation analysis can be done in addition to or instead of an ANOVA. ANOVAs do not tell you how much of an effect the independent variable has on the dependent variable. With an ANOVA test, you can ask the software to provide effect size statistics, which give you some general idea of how much of an effect that x has on y. These are: eta squared (η2), omega squared (ω2), and Cohen's d; these are desribed in the textbook, and in typical statistics courses on ANOVAs.
5.4 Assumptions
The following are assumptions, or basic requirements, for doing an ANOVA, t-tests, standard correlation analyses, and other common statistical tests. # Independence of cases: A subject's response to one item (on a test, in an experiment, etc.) is not (unduly) affected by a previous response; one subject's responses are not affected by another subject's responses.
- Normality: The data fit within a standard, normal distributions (normally distributed).
- Equivalent variances across groups: The different groups will likely have different variances, but within a normal range of variances; you should not see wild, extreme differences in variances between groups (if that happens, one or more groups may not be normally distributed).
- Appropriate data type: Dependent variables should be numerical.
Statistical tests that meet these requirements or parameters are called parametric tests--ANOVAs and related tests, t-tests, Pearson correlation tests, and others. If standard ANOVA assumptions don't apply--for minor violations of these assumptions--alternatives to a regular ANOVA would be non-parametric tests known as the Mann-Whitney or Kruskal-Wallis tests, which are also less powerful, and maybe less able to detect differences (these are discussed briefly in the textbook). Many times for categorical data that are not normally distributed, or not likely to be normally distributed, a non-parametric test like the chi-square test would be preferred. Chi-square tests and logistic regression analysis are especially preferred for dependent variables that are categorical or not fully continuous (numerical).
6 Other tests
There are many variations of the standard ANOVA that are not discussed here, but are discussed in standard books on research design or basics statistics texts--one-way ANOVAs with one independent variable, two-way ANOVAs with two independent variables, as well as so-called Latin square designs and split plot designs. You can look at such texts for more on these. Some of these variations on the ANOVA tests for more complex situations are briefly discussed below--ANCOVA, MANOVA, and repeated measures tests. In addition to these standard ANOVA designs, there are more specialized adaptations of ANOVAs for other needs. In addition, there are tests outside the ANOVA family, whose basic workings are conceptually similar to ANOVAs but more sophisticated and powerful, for more specialized cases where ANVOAs won't work very well, such as GLM and HLM.
6.1 ANCOVA: analysis of covariance
A control variable or covariate is included a factor that you want to control for and factor out first, to separate its influence from that of the main IV. For example, one might want to first calculate and factor out the effects of socioeconomic status (SES) in an analysis of test scores, where SES is known to be a relevant factor, but not one that you're primarily interested in. These covariates are numerical variables (e.g., income level or range for SES).
6.2 Repeated measures ANOVA
The subject responds twice in one session on one type of item--i.e., two or more responses on the same or similar item are collected from the same subject, at a time interval close enough that the second response could be influenced by the first response. For example, reading times on the same word or phrase that is encountered more than once would be a repeated measures. Special adjustments are used in the ANOVA computations for the variance between the time intervals.
6.3 MANOVA
Multiple analysis of variants--to test two dependent variables at once. One can see how independent variables affect two dependent variables at once, and how two dependent variables might be related to each other. This is not often used in language research. Missing data--not having the same number of responses or data for each condition (e.g., if some subjects drop out or don't respond to some items) are more problematic for MANOVAs than for other tests, as MANOVAs do not work well for missing data or groups of unequal sizes.
- y1 + y2 = x1 = x2 + x3 ...
6.4 Time series analysis
Somewhat like an ANOVA or regression model, for measuring events at different times and correlations between times and events (e.g., measuring performance on a particular language skill over time, and including the times as a factor in the equation). More complex analyses would use whats known as a generalized liner model (GLM) instead of a standard ANOVA. GLM is a more sophisticated statistical test that would be preferred, since this handles time variables differently than other variables.
- y = t1(b1x1 ...) + t2 (b1x1 ...)... where t = measurement times
6.5 Hierarchical linear models
HLM (or mixed level model, or multilevel analysis) is even more sophisticated. It is somewhat like an ANOVA or regression model, but for a variety of different kinds individual and group level variables in a more complex statistical model. For example, we might have a complex study with two numerical IVs (like scores on two different tests as IVs), plus the students' classroom as a group variable (g1) and students' school as another group variable (g2), while explicitly factoring out each student's individual variability (r, for subject as random variable). This can handle situations where subjects belong to more than one group or hierarchies of groups (e.g., in an education study, class, grade, school, school district, city), mixtures of fixed and random effect variables (e.g., subject, experimental item, etc.), and other complexities. GLM and HLM are very useful for large and complex data sets. An HLM model might look like this, with group variables [g], regular independent variables [x], regression slopes or correlation estimates [b], and random effects [r] (and a=the intercept; see handout on correlation).
- y = a + g1 + g2 + b1x1 + b2x2 + r
6.6 Chi-square (χ2) tests
In many language research studies, the normal distribution will suffice. Some certain kinds of data do not follow the normal distribution, in which case we may use tests based on the chi-square distribution or other distributions. The chi-square test is based on the chi-square distribution, and involves comparing ratios of actual versus expected outcomes (e.g., values that would be expected if two groups are the same, versus actual values for groups that may be different). It is briefly discussed below and in the textbook, as it is a common alternative for when the parametric assumptions do not hold, e.g, when data do not fit the normal distribution. While the standard normal distribution is always bell-curve-shaped, for these other distributions, the shape of each distribution varies according to the number of subjects or n-size.
For example: A chi-square test is used to compare proportions of two groups, e.g., proportions of patients who improve in a drug treatment group cf. those in a control group. Thus, it is often used for categorical dependent variables, or for group comparisons where standard ANOVA assumptions do not hold.
This is also used for categorical dependent variables, i.e., if the DV pertains to identifying which category an item belongs to; for example, in predicting whether the subject is classified into certain categories.
1. In a medical experiment, the outcome measured is whether the patient responds to a new drug or treatment.
- y = x
- where x = drug dosage (0mg, 100mg, 500mg), and
- y = outcome: no improvement, slight improvement, moderate improvement, great improvement
2. In a survey of how subjects feel about their level of L2 attainment, where numbers on a Likert scale survey represent these categories.
- y = x
- where x = motivation type: pragmatic, general intrinsic, or integrative (social), and
- y = self-perception of L2 attainment: poor, so-so, good, high
A chi-square test can also be used when independent variables are random variables, e.g., in some more advanced procedures when the particular subjects themselves (random effect) are an important variable to be measured and controlled for.
7 Software
Typically, SPSS is a very popular program for doing a number of basic statistical analyses like t-tests, ANOVAs, correlation tests, GLM, and chi-square tests. It is expensive, but has a simple, intuitive graphical interface. SAS is also very good, and provides more options for more complex types of statistics, and better suited for logistic regression and HLM. SAS is also expensive, and lacks the intuitive graphical interface; one typically enters commands instead, but it is easy to work with once you get used to it. Other programs can easily handle these basic statistical procedures, along with more sophisticated ones, like Systat. One increasingly popular program is R, which is free, available on different operating systems (Windows, Linux, MacIntosh), and very powerful--one can add packages to handle any kind of statistical procedure for any kind of work (social science, econometrics, biology, pure math, etc.); however, it uses a fairly complex command language (though there is a fairly new extra module that one can add that provides for a graphical interface).
8 Appendix
| common variables in statistics | |
| x | an independent variable (in modeling equations, like y = x); OR an item score--a specific value for a subject's score or response on the independent variable (e.g., x1, x2, x3 …)
(The Greek letter μ (“mu”) is used if the entire population is known beforehand) |
| x | the mean for a group |
| s (sd) | standard deviation |
| s2 | variance[5] |
| n | the number of items or subjects in a group (sometimes capital N refers to the number of all subjects in an experiments, while n refers to those in a group, or to the number of test items) |
| k | the number of groups in an experiment (e.g., for L1 background as a variable, if we have two L1 groups like Japanese and French, then k=2) |
| e | error--random variation that cannot be explained by known variables |
| other abbreviations (e.g., in data tables or charts | |
| n, N | number of subjects and/or items (see above) |
| SD | standard deviation (sometimes you see SEM, standard error of the mean, which is similar to the SD) |
| M | mean |
For a simple comparison of two groups, the t-test compares different scores between groups [x1, x2...], the standard deviation [s], and the n-size (number of subjects).
An ANOVA works similarly, comparing the sum of squares (variance) overall with those of the different groups, e.g., treatment and control groups (plus error, or variance that can't be explained by the treatment effect).
SStotal = SStreatment + SSerror
This is computed by comparing the overall variance, and the group means and variances.
or
8.1 Other ANOVA outputs
Sometimes in language studies you see two ANOVA outputs, an F1 and an F2. Typically, an ANOVA assumes that the subjects are random variables (though that's not shown in the models like y=x), in terms of how the calculations proceed. That's the standard way, leading to a standard F-score (the F1). However, a second ANOVA may be run on the data, using test items (like the experimental items that the subjects read or responded to) as a random variable instead. That's the second F2 result, and usually the second results usually correspond more or less with the first one. The second ANOVA is done to make sure the test items were reliable and well-designed, and thus did not contribute undue variance, and to provide further evidence for the effect of the independent variable.
Sometimes for mild violations of assumption #3 (for unusual variances), an adjusted F-statistic is used for calculating probability, called Fˊ (F prime), or other adjustments may be made.
8.2 Greek letters for variables
Theoretically, we make a distinction between a factor that we know for a whole population, verses a group of subjects (who theoretically represents a subset of a population), for whom we estimate the values of a variable. A variable that we know for an entire population is called a parameter, and is often indicated with Greek letters. Usually we work with a group of subjects representing a subset, from whom we estimate the values of the variables; these values are indicated with Latin letters. Thus, a mean = x̄, or μ; a standard deviation = s (or sd), or σ (the estimate from a sample is sometimes called the standard error of the mean, or SEM); variance = s2, or σ2.
- ↑ Means are often referred to with the variable x̄, pronounced “x-bar”.
- ↑ These statistical tests are based on the normal distribution, but the statistical calculations may use very slight modifications of the distribution. The t-test uses a form of the normal distribution tweaked for small samples, which is called the Student distribution. ANOVAs use the F-distribution for larger samples, named for R.A. Fisher, one of the founders of modern statistics.
- ↑ To avoid negative signs (like -7), since t-tests and ANOVAs were invented in the early 20th century before calculators existed, this is done by squaring the terms - computing the sum of squares (SS), or ordinary least squares (OLS). Thus, variance was usually calculated and the square root of that taken instead of directly computing the standard deviation, as negative signs were hard to work with before calculators existed. And thus, ANOVA and t-test calculations are actually based on variance. The capital letter sigma [Σ], the summation sign, indicates group sums.
- ↑ Alternatively, the probability level can be expressed in terms of confidence intervals. A probability of p<.05 is equivalent to a confidence interval of CI=95%, that is, one can be 95% sure that the results are significant, i.e., indicative of a meaningful difference between groups or a meaningful effect of the independent variable.
- ↑ If the whole population's characteristics are known beforehand, then Greek letters are used (see Appendix); the letter μ [“mu”] is used for means, σ [“sigma”] for the SD, σ2 for variance, and ν (“nu”) for n-size, ε (“epsilon”) for error, etc.